EKONOMI TEKNIK

Ekonomi Teknik

BAB 4

4.1 ANALISIS INCREMENTAL

Analisis incremental biasanya dinyatakan juga sebagai biaya diferensial, biaya marjinal, atau biaya relevan. Analisis incremental ini fleksibel, dimana data dapat dihitung dan disajikan untuk alternatif keputusan berdasarkan periode, seperti hari, minggu, bulan atau tahun.

Analisis incremental digunakan dalam pengambilan keputusan ketika jumlah dari alternatif keputusan dan keadaan alam sangat besar. Penggunaan tabel payoff atau pohon keputusan mungkin terlalu rumit untuk digunakan, sehingga dalam pengambilan keputusan dilakukan pendekatan yang telah disederhanakan. Pendekatan

ini membantu pemimpin perusahaan untuk melakukan sejumlah keputusan yang tepat

dalam waktu yang relatif singkat. Analisis ini dapat digunakan dalam berbagai bidang, seperti bidang pemasaran atau bidang produksi. Analisis incremental adalah cara pengambilan keputusan di mana biaya operasional atau pendapatan dari satu alternatif dibandingkan dengan alternatif lain. Alternatif keputusan terbaik adalah biaya operasional terkecil atau pendapatan yang terbesar.

Analisis incremental dapat digunakan untuk mengevaluasi alternatif-alternatif keputusan, seperti:

• Menyimpan atau mengganti barang tertentu

• Membuat atau membeli sejumlah barang tertentu

• Menjual sekarang atau memproses barang lebih lanjut

• Menyewa ruangan lain atau melanjutkan kegiatan

• Melanjutkan atau menghentikan produksi

• Menerima atau menolak penawaran khusus

• Perubahan jangka waktu kredit

• Membuka tempat baru

• Membeli atau menyewa, dan lain-lain

Dalam menganalisis perbedaan antara harapan kerugian menyediakan barang pertama  dengan  tidak  menyediakan  barang  pertama,  apabila  penyediaan  barang pertama (first barang) mempunyai nilai harapan kerugian lebih kecil daripada tidak menyediakan  barang  pertama,  kemudian  dilanjutkan  dengan  menggunakan  rumus incremental untuk barang kedua dan seterusnya.  Apabila ternyata penyediaan barang ke-n  mempunyai  nilai  harapan  kerugian  lebih  besar  daripada  tidak  menyediakan barang tersebut, persediaan optimal sudah tercapai dan analisis dihentikan.

Dalam permasalahan persediaan sederhana, misalkan seorang produsen akan memesan  barang  dari  luar  kota  dalam  rentang  waktu  yang  telah  ditentukan  dan barang  yang  telah  dipesan  akan  disimpan  dalam  gudang  penyimpanan.  Rentang waktu yang telah ditentukan  dapat  dibuat dalam hari, minggu, dan lain-lain. Harga pembelian setiap barang sebesar X dan barang tersebut akan dijual sebesar Y. Apabila diakhir rentang waktu yang telah ditentukan terdapat barang yang tidak terjual, maka

barang tersebut akan dijual kembali sebesar Z.  Permintaan barang setiap rentang waktu  yang  telah  ditentukan  berkisar  a1 buah barang sampai an buah  barang. Banyaknya rentang waktu yang dibutuhkan untuk menjual setiap barang sebanyak b1 sampai bn. Probabilitas  hasil penjualan p1   sampai setiap barang adalah banyaknya rentang waktu penjualan barang                              

Hasil perhitungan ditunjukkan dengan tabel berikut

Penjualan Barang (pcs)	Banyaknya Rentang Waktu Penjualan	Probabilitas
A1 A2 : An	B1 B2 : Bn	P1 P2 : Pn
JUMLAH		1

• Membuka tempat baru

• Membeli atau menyewa, dan lain-lain

PWbiaya = PWkeuntungan

Atau    PWbiaya – PWkeuntungan = 0

Atau     NPW = 0 (net present worth = 0 ).

Jika menggunakan EUAC:

EUAC = EUAB

atau     EUAC – EUAB = 0

atau     NAW (net annual worth) = 0

Contoh :

Pengendalian material disuatu pabrik dilakukan secara manual. Biaya yang diperlukan

untuk gaji karyawan yang mengoperasikan pengendalian material tersebut (termasuk gaji lembur, asuransi, biaya cuti dan sebagainya) ditaksir tiap tahun Rp. 9.200.000.

Pengendalian secara manual ini disebut alternatif A. Untuk menekan gaji karyawan yang cenderung meningkat, pabrik tersebut ingin mengganti pengendalian material tersebut dengan otomatis ingin mengganti pengendalian material tersebut dengan yang otomatis (alternatif B) yang harganya adalah Rp. 15.000.000. Dengan menggunakan pengendalian otomatis tersebut, gaji karyawan ditaksir akan berkurang menjadi

Rp. 3.300.000 tiap tahun. Biaya pengoperasian yang terdiri atas biaya listrik, pemeliharaan dan pajak masing-masing-masing tiap tahun adalah Rp. 400.000, Rp.1.100.000, dan Rp. 300.000. Jika pengendalian otomatis yang digunakan ada pajak ekstra sebesar Rp. 1.300.000 tiap tahun. Pengendalian otomatis tersebut dapat dipakai selama 10 tahun dengan nilai akhir nol. Jika suku bunga i = 9% (MARR), tentukan alternatif mana yang dipilih. Pertama-tama dibuat terlebih dahulu tabel aliran kas tersebut :

NPW = 0 = -15.000.000 + 2.800.000 (P/A, i%, 10)

Atau NAW = 0 = -15.000.000 (A/P, i%, 10) + 2.800.000

Dengan cara coba-coba diperoleh i = 13,3%.

Karena i = 13,3% > 9% maka pilih alternatif B karena lebih ekonomis.

Jika digunakan perhitungan EUAC maka diperoleh :

EUAC (A) = Rp. 9.200.000

EUAC (B) = 15.000.000 (A/P, 9%, 10) + 3.300.000 + 400.000 + 1.100.000 + 300.000

+ 300.000

= Rp. 8.737.000.

Hasilnya konsisten dengan perhitungan PW, bahwa EUAC (B) < EUAC (A).

4.2 BENEFIT COST RATIO

Benefit cost ratio (B/C R) merupakan suatu analisa pemilihan proyek yang biasa  dilakukan karena mudah, yaitu perbandingan antara benefit dengan cost. Kalau nilainya < 1 maka proyek itu tidak ekonomis, dan kalau > 1 berarti proiyek itu feasible. Kalau B/C ratio = 1 dikatakan proyek itu marginal (tidak rugi dan tidak untung).

Benefit dan cost tetap

Misalnya suatu pryek pengairan mempunyai umur ekonomis 30 tahun, investasi awal  pada  awal  tahun  pertama  adalah  Rp  1  milyar  sedang  biaya  OP  Rp  20 juta/tahun, keuntungan proyek adalah Rp 126 juta/tahun. Bunga bank 5 %, maka :

Biaya tahunan :

Bunga bank 5%                       Rp 50 juta

Depresiasi 30 tahun                 Rp 15 juta

OP                                           Rp 20 juta

Total biaya tahunan                             Rp 85 juta

Benefit per tahun                                Rp 126 juta

B/C ratio = 126/85 = 1,48

Seperti pada contoh di atas, capital cost Rp 1 milyar, annual benefit Rp 126 juta, annual OP Rp 20 juta.

Benefit dan cost tidak tetap

Kalau benefit  dan  cost tidak sama  tiap tahunnya  maka  analisa  dilakukan bedasarkan  nilai sekarang (present value) atau nilai yang akan datang (future value) pada suatu waktu  tertentu. Yang mempengaruhi nilai B/C ratio adalah besarnya bunga bank. Semakin rendah nilai bunga bank semakin tinggi nilai B/C ratio.

Kalau OP dianggap sebagai yang mengurangi jumlah benefit tiap tahunnya, maka  nilai  B/C ratio berubah. Misalnya pada bunga 5%, total biaya tahunan menjadi Rp 65 juta dan benefit tahunan menjadi Rp 126 juta – Rp 20 juta = Rp106 juta sehingga nilai B/C ratio menjadi 106/65 = 1,63

Kalau ratio dihitung dengan tetap memperhitungkan biaya OP tahunan, maka disebut B/C  ratio. Sedangkan kalau biaya OP dikurangkan pada benefit maka disebut B/C* ratio. Jadi harus dijelaskan cara mana yang akan dipakai.

Net benefit

Net benefit  adalah  benefit  dikurangi  cost.  Untuk  beneifit  dan  cost  yang konstan  maka  net  benefit  tahunan  adalah  selisih  dari  kedua  parameter  ini, sedangkan untuk benefit dan cost yang tidak konstan, selisih harus dihitung atas present  value  atau  future  value  pada  waktu  yang  sama.  Pengurangan  benefit dengan biaya OP tidak mempengaruhi net benefit. Sebagai contoh pada bunga 5

% benefit dikurangi OP = Rp 106 juta sedang biaya tahunan Rp 65 juta maka net benefit = Rp 106 juta – Rp 65 juta = Rp 41 juta sama kalau benefit tahunan tidak dikurangi dengan biaya OP tahunan, yaitu Rp 126 juta – Rp 85 juta = Rp 41 juta.

Benefit Cost Ratio Analysis merupakan teknik analisa dalam mengetahui nilai manfaat dari sebuah proyek yang akan dijalankan. Yakni membandingkan antara nilai manfaat dengan nilai investasi/ modal.

PW of Benefit – PW of Cost ≥ 0 atau EUAB – EUAC ≥ 0

 sehingga kriteria yang di ambil baik untuk fixed input maupun fixed output sama-sama yang menghasilkan maksimum B/C.

Contoh:
Perusahaan mencoba melakukan modifikasi terhadap alat berat untuk me-reduce pengeluaran dengan mengganti komponen alat X dan komponen alat Y. Biaya penginstalan masing-masing $1.000 dan umur manfaat sampai 5 tahun dan diakhir tahun tidak mempunyai nilai sisa. Komponen alat X menghemat $300 pertahunnya dan komponen Y menghemat $400 di tahun pertama dan menurun $50 di tahun berikutnya. Jika suku bunga 7% komponen mana yang akan di beli perusahaan?

Penyelesaian:

Komponen X:
PW of cost                  = $1.000
PW of Benefit             = 300 (P/A,7%,5) = 300 (4,100) = $ 1230
B/C                              = PW of Benefit / PW of Cost = 1230 / 1000 = 1,23

Komponen Y:
PW of cost                  = $1.000
PW of Benefit             = 400 (P/A,7%,5) – 50 (P/G,7%,5) = 400 (4,100) – 50 (7,647)

                                    = 1640 – 382 = $ 1258
B/C                              = PW of Benefit / PW of Cost = 1258 / 1000 = 1,26

Maksimal B/C, pilih komponen Y

4.3 ANALISA PAYBACK PERIOD

Periode pengembalian – payback period

Periode “Payback” menunjukkan berapa lama (dalam beberapa tahun) suatu investasi akan bisa kembali. Periode “Payback” menunjukkan perbandingan antara “initial investment” dengan aliran kas tahunan, dengan rumus umu sebagai berikut :

Payback Period =   Nilai Investasi

                                    Proceed

Apabila periode payback kurang dari suatu periode yang telah ditentukan proyek tersebut diterima, apabila tidak proyek tersebut ditolak. Jangka waktu yang dibutuhkan untuk mengembalikan nilai investasi melalui penerimaan – penerimaan yang dihasilkan oleh proyek investasi tersebut juga untuk mengukur kecepatan kembalinya dana investasi.

Kebaikan Payback Method

1. Digunakan untuk mengetahui jangka waktu yang diperlukan untuk pengembalian investasi dengan resiko yang besar dan sulit.
2. Dapat digunakan untuk menilai dua proyek investasi yang mempunyai rate of returndan resiko yang sama, sehingga dapat dipilih investasi yang jangka waktu pengembaliannya cepat.
3. Cukup sederhana untuk memilih usul-usul investasi.

Kelemahan Payback Method

1. Tidak memperhatikan nilai waktu dari uang.
2. Tidak memperhitungkan nilai sisa dari investasi.
3. Tidak memperhatikan arus kas setelah periode pengembalian tercapai.

Rumus periode pengembalian jika arus kas per tahun jumlahnya berbeda :

Payback Period = n + a – b  x 1 tahun

                                                c – b

n = Tahun terakhir dimana jumlah arus kas masih belum bisa menutup investasi awal

a = Jumlah investasi mula-mula

b = Jumlah kumulatif arus kas pada tahun ke – n

c = Jumlah kumulatif arus kas pada tahun ke n + 1

Rumus periode pengembalian jika arus kas per tahun jumlahnya sama :

Payback Period = Investasi awal x 1 tahun

                                    Arus kas

· Periode pengembalian lebih cepat : layak

· Periode pengembalian lebih lama : tidak layak

· Jika usulan proyek investasi lebih dari satu maka periode pengembalian yang lebih cepat yang dipilih

Contoh kasus arus kas setiap tahun jumlahnya berbeda

Suatu usulan proyek investasi senilai Rp. 600 juta dengan umur ekonomis 5 tahun, Syarat periode pengembalian 2 tahun, dengan tingkat bunga 12% per tahun, dan arus kas pertahun adalah :

· Tahun 1 RP. 300 juta

· Tahun 2 Rp. 250 juta

· Tahun 3 Rp. 200 juta

· Tahun 4 Rp. 150 juta

· Tahun 5 Rp. 100 juta

Arus kas dan arus kas kumulatif

Tahun	Arus kas	Arus kas kumulatif
1	300.000.000	300.000.000
2	250.000.000	550.000.000
3	200.000.000	750.000.000
4	150.000.000	900.000.000
5	100.000.000	1.000.000.000

Payback Period = n + a – b  x 1 tahun

           c – b

= 2 + Rp 600jt – Rp 550jt x 1 tahun

Rp 750jt – Rp 550jt

= 2,25 tahun atau 2 tahun 3 bulan

4.4 BREAK EVENT POINT

Break Even point atau BEP (titik impas) adalah suatu kondisi dimana jumlah pendapatan dan jumlah pengeluaran adalah seimbang, sehingga tidak terdapat kerugian atau keuntungan. Hal tersebut dapat terjadi bila perusahaan dalam operasinya menggunakan biaya tetap, dan volume penjualan hanya cukup untuk menutup biaya tetap dan biaya variabel. Apabila penjualan hanya cukup untuk menutup biaya variabel dan sebagian biaya tetap, maka perusahaan menderita kerugian. Dan sebaliknya akan memperoleh memperoleh keuntungan, bila penjualan melebihi biaya variabel dan biaya tetap yang harus di keluarkan.

Manfaat BEP

Analisis Break even secara umum dapat memberikan informasi kepada pimpinan, bagaimana pola hubungan antara volume penjualan, cost/biaya, dan tingkat keuntungan yang akan diperoleh pada level penjualan tertentu. Analisis break even dapat membantu pimpinan dalm mengambil keputusan mengenaihal-hal sebagai berikut:

1. Jumlah penjualan minimalyang harus dipertahankanagar perusahaan tidak mengalami kerugian.
2. Jumlah penjualan yang harus dicapai untuk memperoleh keuntungan tertentu.
3. Seberapa jauhkah berkurangnya penjualan agar perusahaan tidak menderita rugi.

4.      Untuk mengetahui bagaimana efek perubahan harga jual, biaya dan volume penjualan terhadap keuntungan yang diperoleh.

Menurut Sutrisno analisa Break Even dapat digunakan untuk membantu menetapkan sasaran tujuan perusahaan, kegunaan bagi menejemen antara lain :

1. Sebagai dasar atau landasan merencanakan kegiatan operasional dalam usaha mencapai laba tertentu
2. Sebagai dasar atau landasan untuk mengendalikan kegiatan operasi yang sedang berjalan yaitu alat untuk pencocokan antara realisasi dengan angka-angka dalam perhitungan Break Even atau dalam gambar Break Even .
3. Sebagai bahan pertimbangan dalam penentuan harga jual yaitu setelah diketahui hasil perhitungan menurut hasil analisa Break Even dan laba yang ditargetkan.
4. Sebagai dasar pertimbangan dalam pengambilan keputusan yang harus dilakukan seorang manager suatu perusahaan.

Manfaat Break Even Point dari berbagai segi seperti keuangan, kuantitas yang diproduksi, perubahan harga penjualan, dan dari segi laba adalah sebagai berikut :

1. BEP bermanfaat bagi perusahaan untuk mengetahui kondisi keuangan perusahaan
2. BEP bermanfaat bagi perusahaan untuk menentukan jumlah peralatan dalam rupiah atau unit yang akan dihasilkan perusahaan agar tidak rugi dan tidak untung.
3. BEP bermanfaat untuk menargetkan perusahaan harga penjualan dan peralatan.
4. BEP bermanfaat untuk mengetahui jumlah biaya tetap dan variabel serta hubungan pendapatan total pada tingkat produksi.

Contoh :

Andaikan bahwa diperlukan motor bertenaga 20 TK untuk memompa air dari suatu sumber air. Banyak jam beroperasi (jam motor bekerja) tiap tahun tergantung pada t ingi curah hujan (jadi merupakan suatu variabel). Motor tersebut diperlukan untuk jangka waktu 4 tahun. Untuk penyediaan motor tersebut telah diusulkan 2 alternatif.

Alternatif A memerlukan biaya awal untuk pembelian motor listrik yang bekerja secara otomatis dengan harga Rp 1.400.000 dan nilai akhirnya pada akhir tahun keempat ditaksir Rp 200.000. Biaya pengoperasian tiap jam Rp 840, dan biaya pemeliharaan tiap tahun ditksir Rp 120.000. Alternatif B memerlukan biaya awal untuk pembelian motor gaselin Rp 550.000 dan nilai akhir nol pada akhir periode tahun keempat.

Biaya bahan bakar untuk tiap jam operasi ditaksir Rp 420 ; biaya pemeliharaan ditaksir Rp 150 tiap jam dan biaya operator tiap jam Rp 800. Akan ditentukan berapa jam tiap tahun kedua motor tersebut beroperasi agar biaya kedua altenatif tersebut sama. Gunakan i (MARR) 10 %

Penyelesaian :

Misal   TCA    = total EUAC (A)

CRA                = Capital recovery cost alternatif A

= (1.400.000 – 200.000) (A/P,10%,4) + 200.000 (0,10) = 399.000

MA                  = biaya pemeliharaan tiap tahun untuk alternatif A

= Rp. 120.000

CA                              = biaya pengoperasian tiap jam = Rp 840

t                       = jumlah jam operasi tiap tahun

Maka   TCA    = CRA + MA + CA t

TCB                            = total FUAC (B)

CRB                = Capital recovery cost alternatif B

= Rp. 550.000 (A/P, 10%, 4) = Rp. 174.000

HB                              = biaya t iap jam dar i penggunaan gaselin + operator + pemeliharaan

= Rp 420 + Rp 800 + Rp 150 = Rp 1370

t                       = jumlah jam operasi tiap tahun.

Maka TCB = CRB + Ht.

Untuk mendapatkan titik impas adalah dengan menyelesaikan t dari persamaan.

TCA = TCB

atau CRA + MA + CAt = CRB + HBt

diperoleh:

Jadi kedua motor tersebut sama ekonomisnya jika kedua motor tersebut beroperasi selama 651 jam dalam setahun. Jika digunakan kurang dari 651 jam maka motor gasolin lebih ekonomis dan jika digunakan lebih da r i 651 jam motor listrik lebih ekonomis. Gambar ini menunjukkan total biaya tiap tahun sebagai fungsi dari banyaknya jam bekerja tiap tahun.

Perbedaan biaya tahunn antara kedua alternatif tersebut untuk sembarang jam operasi tertentu dapat dihitung sebagai berikut :

Misalnya kedua motor dioperasikan 100 jam tiap tahun maka :

TC  = TCA – TCB

= CRA + MA + CAt – CRB – HBt

= 399.000 + 120.000 + 100 (0,84) – 174 – 100 (1,37)

= Rp. 292.000

4.5 ANALASIS SENSIVITAS

Nilai-nilai parameter dalam studi ekonomi teknik biasanya diestimasikan besarnya, akibatnya nilai-nilai tersebut mempunyai factor kesalahan. Mungkin lebih besar atau lebih kecil dari hasil estimasi yang diperoleh atau berubah pada saat-saat tertentu. Perubahan yang terjadi pada nilai-nilai parameter akan mengakibatkan perubahan pada hasil yang ditunjukkan oleh suatu alternative investasi. Perubahan ini memungkinkan keputusan akan berubah dari satu alternative ke alternative yang lain. Apabila berubahnya factor-faktor atau parameter-parameter tersebut mengakibatkan berubahnya suatu keputusan, maka keputusan tersebut dikatakan sensitive terhadap perubahan nilai parameter atau factor tersebut. Untuk mengetahui seberapa sensitive suatu keputusan terhadap perubahan faktora atau parameter yang mempengaruhinya maka setiap pengambilan keputusan seharusnya disertai dengan analisa sensitivitas. Analisa sensitivitas akan memberikan gambaran sejauh mana suatu keputusan akan konsisten meskipun terjadi perubahan factor-faktor

atau parameter-parameter yang mempengaruhinya. Analisa sensitivitas dilakukan dengan mengubah nilai suatu parameter pada suatu saat untuk selanjutnya dilihat bagaimana pengaruhnya terhadap akseptabilitas suatu alternative investasi. Parameter-parameter yang biasanya berubah dan perubahannya dapat mempengaruhi keputusan adalah biaya investasi, aliran kas, nilai sisa, tingkat bunga, tingkat pajak, dan sebagainya.

Analisis sensitivitas merupakan analisis yang berkaitan dengan perubahan diskrit parameter untuk melihat berapa besar perubahan dapat ditolerir sebelum solusi optimum mulai kehilangan optimalitasnya. Jika suatu perubahan kecil dalam parameter menyebabkan perubahan drastis dalam solusi, dikatakan bahwa solusi sangat sensitive terhadap nilai parameter tersebut. Sebaliknya, jika perubahan parameter tidak mempunyai pengaruh besar terhadap solusi dikatakan solusi relative insensitive terhadap nilai parameter itu. 

Dalam membicarakan analisis sensitivitas, perubahan-perubahan parameter dikelompokan menjadi:

1. Perubahan koefisien fungsi tujuan
2. Perubahan konstan sisi kanan
3. Perubahan batasan atau kendala
4. Penambahan variable baru
5. Penambahan batasan atau kendala baru.

BAB 5

5.1 DEPRESIASI

Depresiasi atau penyusutan modal adalah suatu komponen yang penting dalam analisis ekonomi teknik, terutama dalam analisis yang berkaitan dengan pajak dan pengaruh inflasi (after tax and inflation analysis). Secara umum depresiasi dapat didefinisikan sebagai berkurangnya nilai suatu asset (yang dapat berupa mesin-mesin, bangunan gedung dll) sesuai dengan waktu. Depresiasi secara umum dapat digolongkan dalam 2 kelompok, yaitu:

1.Depresiasi yang disebabkan antara lain mesin-mesin atau peralatan-peralatan yang digunakan semakin tua sehingga kemanpuannya berkurang (physical degradation).

2.Depresiasi yang disebabkan antara lain karena semakin majunya perkembangan teknologi, sehingga diperlukan mesin-mesin atau peralatan-peralatan baru yang lebih efisien dan ekonomis daripada yang dipakai sekarang atau karena adanya perubahan demand di masya r akat baik dari segi kualitas maupun kuantitas sehingga diperlukan tambahan mesin-mesin dan peralatan-peralatan baru (functional depreciation).

Untuk memahami konsep depresiasi bukanlah suatu hal yang mudah, karena disini memuat 2 pengertian yang harus dipertimbangakan. Yang pertama, yaitu depresiasi nilai asset yang sebanarnya sesuai dengan waktu dan yang kedua (yang penting dalam ekonomi teknik) yaitu bagaimana mengalokasikan depresiasi (accounting depreciation) nilai asset tersebut.

Dalam mengalokasikan depresiasi nilai asset ada 2 hal yang dipertimbangkan yaitu:

-Untuk menjamin bahwa asset yang diinvestasikan dapat diperoleh kembali selama umur ekonomisnya:

-Untuk menjamin bahwa asset yang. diinvestasikan diperhitungkan sebagai biaya produksi, sehingga berkaitan dengan pajak.

Untuk menghitung depresiasi, ada 3 komponen utama yang digunakan, yaitu : nilai asset (P), umur teknis(n), dan nilai akhir (S). Metode depresiasi dapat diklasifikasikan sebagai berikut:

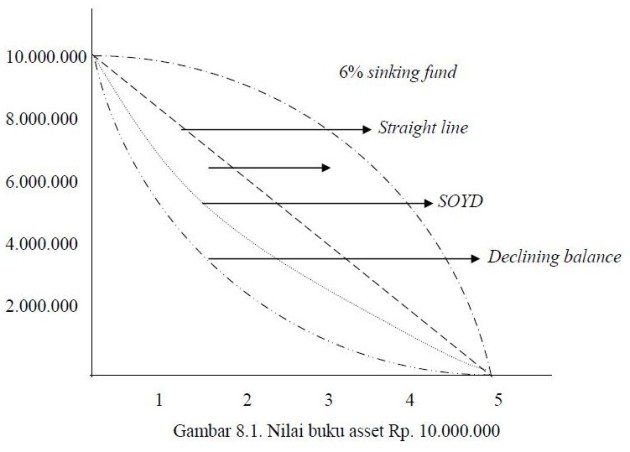
Metode yang bertujuan untuk mengalokasikan depresiasi yang lebih besar pada awal umur teknis daripada akhir umur teknis. Metode yang digunakan antara lain: declining balance depreciation accounting, dan Sum of Years digits depreciation accounting (SOYD).

Metode yang bertujuan untuk mengalokasikan depresiasi secara merata selama umur teknis. Metode yang digunakan adalah straight line depreciation accounting.

Metode yang bertujuan untuk mengalokasikan depresiasi yang lebih besar pada akhir umur teknis daripada awal umur teknis. Metode yang digunakan adalah sinking – fund depreciation accounting.

Straight line depreciation accounting

Besarnya depresiasi pada tahun ke t dengan metode ini diberikan oleh rumus :

dimana d adalah laju depresiasi.

Contoh 1 :

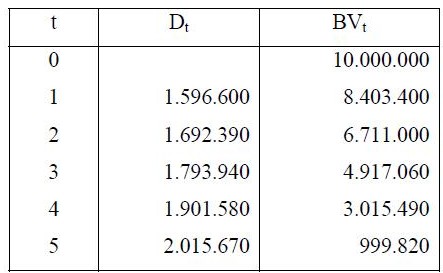
Misal P = Rp. 10.000.000, S = 1.000.000 dan n = 5 tahun

BVt adalah nilai buku pada tahun ke t yang besarnya adalah BVt -1 - Dt, dimana BV0 = P, dan dapat dibuktikan bahwa:

DECLINING – BALANCE Depreciation Accounting

Dalam metode ini besarnya depresiasi pada awal-awal tahun pemakaian lebih besar dari pada akhir tahun pemakaian. Karena diharapkan misalnya mesin-mesin yang baru dapat memeberikan produktivitas yang lebih tinggi pada awal pemakainnya daripada akhir pemakaiannya. Dalam metode ini, untuk laju depresiasi tertentu, besarnya depresiasi adalah perkalian laju depresiasi dengan nilai buku pada periode bersangkutan.

Contoh 2 :

Lihat kembali contoh 1.

Misal digunakan laju depresiasi 40%.

Konstanta k biasanya adalah 1,25 ; 1,5 ; 2,0. Jika k = 2 seperti contoh 2. disebut double declining balance depreciation.

Besarnya depresiasi pada tahun ke t adalah :

Dt = dr (BVt-1)

Dan     BVt-1 = P (1- dr)t-1

Sum of Years digits (SOYD) depreciation accounting

Metode ini berdasarkan jumlah bilangan tahun, dimana nilai suatu asset berkurang sebanding dengan unit tahunnya.

Contoh 3:

Lihat kembali contoh 1.

Jumlah unit tahun = 1 + 2 + 3 + 4 + 5 = 15

Sinking – fund depreciation accounting

Dalam metode ini di andaikan nilai dari asset berkurang pada saat laju depresiasi bertambah.

Contoh 4:

Lihat kembali contoh 8.1 dan digunakan sinking fund 6 %. Sinking fund depreciation pada tahun :

Pertama       :   (10.000.000 – 1.000.000) (A/F, 6%, 5) = 1.596.600

Kedua         :   1.596.600 + 0,06 (1.596.600) = 1.692.390

Ketiga         :   1.692.390 + 0,06 (1.692.390) = 1.793.940

Keempat      :   1.793.940 + 0,06 (1.793.940) = 1.901.580

Kelima         :   1.901.580 + 0,06 (1.901.580) = 2.015.670

Secara umum :

Dt = (P-S) (A/F, i%, n) + i (P-S) (A/F, i%, n) (F/A, i , t-1)

Setelah disederhanakan diperoleh :

Dt = (P-S) (A/F, i, n) (F/P, i, t-1)

BVt = P-(P-F) (A/F, i, n) (F/A, i, t)

Contoh Soal :

Suatu investasi pada peralatan seharga Rp. 36.000.000 diharapkan dapat menghemat pengeluaran perusahaan sebesar Rp. 8.900.000 tiap tahun untuk selama 8 tahun dan ditaksir nilai akhirnya sama dengan nol pada akhir tahun ke 8. Dengan menggunakan pajak pendapatan (income tax rate) sebesar 48 %, hitung rate of return investasi tersebut dengan menggunakan kondisi-kondisi berikut :

Sebelum pajak pendapatan (before income tax).

Setelah pajak pendapatan dengan menggunakan straight line depreciation.

Setelah pajak pendapatan dengan SOYD.

Setelah pajak pendapatan dengan menggunakan double rate declining balance depreciationuntuk 4 tahun pertama dan 4 tahun berikutnya digunakan straight line depreciation.

Setelah pajak pendapatan dengan SOYD dan ITC (investuen tax credit) sebesar 10% diterapkan langsung.

Setelah pajak pendapatan dengan mengadaikan semua investasi dihapuskan untuk tujuan pajak.

Setelah pajak pendapatan dengan menggunakan depresiasi ACRS (accelerated cost recovery system), lihat Tabel (apendik) dan ITC sebesar 10 % diterapkan langsung.

Setelah pajak pendapatan dengan mengandaikan investasi dihapuskan sebesar 20 % tiap tahun untuk 5 tahun dan ITC sebesar 10 % diterapkan langsung.

Setelah pajak pendapatan dengan menggunakan depresiasi ACRS untuk 5 tahun mulai 1986 dan ITC sebesar 10 % diterapkan langsung.

Penyelesainnya :

a. Sebelum pajak

NPW = 0 = – 36.000.000 + 8.900.000 (P/A. i %, 8)

Dengan cara interpolasi (trial and error) diperoleh i = 18,3 %.

b. Dt = (P-S)/n = 36.000.000 / 8 = 4.500.000

Dibuat terlebih dahulu aliran kasnya :

NPW = 0 = – 36.000.000 + 6.778.000 (P/A, i %, n)

Dengan interpolasi diperoleh i = 10,2 %.

c. Setelah pajak pendapatan dengan SOYD :

NPW = 0 = – 36.000.000 + 8.468.000 (P/A, i %, 8) – 480.000 (P/G, i %, 8)

Dengan interpolasi diperoleh i = 11,2 %.

d. dr = 2 / n= 0,25

Dihitung terlebih dahulu depresiasinya dengan double rate declining balance depreciation untuk 4 tahun pertama.

BV0 = 36.000.000, D1 = dr BV0 = 0,25 (36.000.000) = 9.000.000

BV1 = P (1 – dr) = 36.000.000 (1 – 0,25) = 27.000.000, D2 = dr BV1 = 0,25 (27.000.000) = 6.750.000

BV2 = P (1 – dr2) = 36.000.000 (1-0,25)2 = 20.250.000

d3 = 0,25 BV2 = 50.625.500

BV3 = 36.000.000 (1-0,25)3 = 15.187.500

D4 = 0,25 BV3 = 3.797.000

BV4 = 36.000.000 (1-0,25)4 = 11.390.500

BV4 = merupakan P untuk straight line depretation, yaitu :

Dt = (11.390.500 – 0) / 4=  2.848.000, untuk t = 5, 6, 7, 8.

NPW = 0 = – 36.000.000 + 5.995.000 (P/A, i %, 8) + CFt – 5.995.000) (P/F, i %, t)

Dengan interpolasi diperoleh i = 11,1 %.

e. 

ITC = 10 % (36.000.000) = 3.600.000

NPW = 0 = – 32.000.000 + 8.468.000 (P/A, i %, n) – 480.000 (P/G, i %, 8)

Dengan interpolasi diperoleh i = 14,6 %.

f.

g. dari tabel di atas :

Depresiasi pada tahun   Pertama  = 0,15 (36.000.000) = 5.400.000

Kedua    = 0,22 (36.000.000) = 7.920.000

Ketiga    = 0,21 (36.000.000) = 7.560.000

Keempat = 0,21 (36.000.000) = 7.560.000

Kelima    = 0,21 (36.000.000) = 7.560.000

Dengan interpolasi diperoleh i = 14,7 %

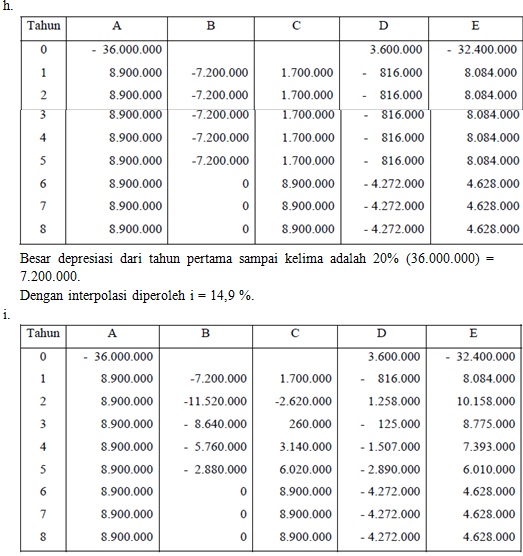
Besarnya depresiasi pada  Tahun pertama = 20 % (36.000.000) = 7.200.000

Tahun kedua = 32 % (36.000.000) = 11.520.000

Tahun ketiga = 24 % (36.000.000) = 8.640.000

Tahun keempat = 16 % (36.000.000) = 5.760.000

Tahun kelima = 8 % (36.000.000) = 2.880.000

Dengan interpolasi diperoleh i = 15,6 %.

BAB 5

5.2 UMUR EKONOMIS

Umur ekonomis adaah depresiasi atau penyusutan dalam akutansi adalah penyebaran biaya asal suatu aktiva tetap (bangunan, alat, komputer, dll) selama umur perkiraannya. Penerapan depresiasi akan mempengaruhi laporan keuangan, termasuk penghasilan kena pajak suatu perusahaan. Metode yang paling mudah dan paling sering digunakan untuk menghitung penyusutan adalah metode penyusutan garis lurus (straight-line depreciation). Tapi selain itu, ada pula metode penghitungan lain yang bisa juga digunakan, seperti metode penyusutan dipercepat, penyusutan jumlah angka tahun, dan saldo menurun ganda. Umur ekonomi menurut kegunaannya dibagi menjadi dua jenis, yaitu :

1.    Umur ekonomi aset baru

Umur ekonomi aset akan meminimasi ekuivalen biaya tahunan seragam (equivalent uniform annual cost – EUAC) kepemilikan dan pengoperasian aset. Sangat penting untuk mengetahui umur ekonomi aset baru (penantang) berdasarkan prinsip bahwa aset baru dan aset lama harus dibandingkan berdasarkan umur ekonomi (optimum) mereka.

MENENTUKAN UMUR EKONOMI ASET BARU (PENANTANG)

Sangat penting mengetahui umur ekonomi, EUAC minimum dan total biaya tahun demi tahun atau biaya tambahan untuk aset baru maupun aset lama sehingga keduanya dapat dibandingkan berdasarkan evaluasi terhadap umur ekonomi dan biaya yang paling hemat keduanya.Untuk sebuah aset baru, umur ekonominya dapat dihitung jika investasi modal,biaya tahunan dan nilai pasar per tahun diketahui atau dapat diestimasi.

Analisis sebelum pajak :

PWk (i%) = I – MVk (P/F,i%,k) + SEj (P/F,i%,j)

TCk (i%) = MVk-1 – MVk + iMVk-1 + Ek

Contoh

Sebuah truk forklift baru akan memerlukan investasi sebesar $20.000 dan diharapkan memiliki nilai pasar akhir tahun serta biaya tahunan seperti diperlihatkan pada tabel dibawah ini. Jika MARR sebelum pajak adalah 10% per tahun, berapa lama aset tersebut harus dipertahankan kegunaannya?

tahun,k	Biaya penggunaan pada tahun, k					EUAC tahun k
	(2)MV, akhir tahun, k	(3)Penyusutan aktual selama tahun, k	(4)Biaya modal = 10% dari MV awal tahun	(5)Biaya tahunan (Ek)	(6) = (3)+(4)+(5)Total biaya (marginal) tahun k (TCk)	(7)EUACk=[STCj(P/F,10%,j)](A/P,10%,k)
0	$20.000	-	-	-	-	-
1	15.000	$5.000=20.000-15.000	$2.000= 20.000×0,1	$2.000	$9.000	$9.000
2	11.250	3.750=15.000-11.250	1.500= 15.000×0,1	3.000	8.250	8.643
3	8.500	2.750=11.250-8500	1.125=11.250×0,1	4.620	8.495	8.600® EUAC minimum (N*=3)
4	6.500	2.000=8500-6500	850=8500×0,1	8.000	10.850	9.082
5	4.750	1.750=6500-4750	650=6.500×0,1	12.000	14.400	9.965

Asumsi : semua arus kas terjadi pada setiap akhir tahun.

Kolom 3 : Penyusutan aktual untuk setiap tahun adalah perbedaan antara nilai pasar awal dan akhir tahun. Penyusutan untuk masalah ini tidak dihitung berdasarkan metode formal namun didasarkan pada hasil kekuatan ekspektasi pasar.

Kolom 4 : Opportunity cost modal pada tahun k adalah 10% dari modal yang tidak direcover (diinvestasikan dalam aset) pada awal masing-masing tahun.

Kolom 7 : Equivalent uniform annual cost (EUAC) yang akan timbul setiap tahun jika aset tersebut dipertahankan penggunaannya sampai tahun k, dan selanjutnya digantikan pada akhir tahun. EUAC minimum terjadi pada akhir tahun N*. ® Pada aset disini memiliki EUAC minimum jika dipertahankan kegunaannya hanya selama tiga tahun (yaitu N*=3).

EUAC2 (10%) = $20.000(A/P,10%,2)-$11.250(A/F,10%,2) + [$2.000(P/F,10%,1) + $3.000(P/F,10%,2)](A/P,10%,2)

= $8.643

2.    Umur ekonomi aset lama

Pembandingan aset baru dengan lama harus dilakukan secara hati-hati karena melibatkan umur yang berbeda. Aset lama harus dianggap memiliki umur lebih lama dibanding umur ekonomi sebenarnya sepanjang biaya marginalnya kurang dari EUAC minimum aset baru.

MENENTUKAN UMUR EKONOMI ASET LAMA

Jika tidak ada MV aset lama saat ini atau nanti (dan tidak ada pengeluaran untuk perbaikan) dan jika biaya operasi aset lama diperkirakan akan meningkat setiap tahun, maka sisa umur ekonomi yang menghasilkan EUAC paling kecil akan satu tahun.

Jika MV lebih besar dari nol dan diharapkan menurun dari tahun ke tahun, maka perlu dilakukan perhitungan sisa umur ekonomi. Penundaan (postponement) umumnya diartikan sebagai penundaan keputusan mengenai kapan akan melakukan penggantian, bukan mengenai keputusan untuk menunda penggantian sampai tanggal masa datang tertentu.

Contoh

Misalnya ingin diketahui berapa lama sebuah truk forklift harus dipertahankan kegunaannya sebelum diganti dengan truk forklift baru yang data-datanya diberikan pada contoh 3. Truk lama dalam kasus ini sudah berusia dua tahun, yang dibeli dengan biaya $13.000 dan memiliki MV yang dapat dicapai saat ini (realizable MV) sebesar $5.000. Jika dipertahankan, nilai pasar dan biaya tahunannya diperkirakan akan seperti berikut :

Akhir tahun k	MV akhir tahun k	Biaya tahunan, Ek
1	$4.000	$5.500
2	3.000	6.600
3	2.000	7.800
4	1.000	8.800

Tentukan periode paling ekonomis untuk tetap mempertahankan aset lama sebelum menggantinya dengan aset pengganti yang ada pada contoh 3. Biaya modal adalah 10% per tahun.\

Jawaban :

Penentuan umur ekonomi aset lama

(1)Akhir tahun, k

(2)Penyusutan aktual selama tahun k

(3)Biaya modal = 10% dari MV awal tahun (*)

(4)Biaya tahunan (Ek)

(5)Total biaya (marjinal) atau tahun (TCi)

=(2)+(3)+(4)(6)EUAC sampai tahun k1$1.000$500$5.500$7.000$7.00021.0004006.6008.0007.47431.0003007.8009.1007.96641.0002008.80010.0008.406

(*) tahun satu berdasarkan MV yang dapat dicapai sebesar $5.000

Perhatikan bahwa EUAC minimum sebesar $7.000 berkaitan denganmempertahankan aset lama satu tahun lagi. Namun, biaya marjinal mempertahankan truk untuk tahun kedua adalah sebesar $8.000, yang masih tetap lebih kecil dari EUAC minimum aset pengganti (yaitu $8.600 dari contoh 3). Biaya marjinal untuk mempertahankan aset lama pada tahun ketiga dan tahun selanjutnya lebih besar dari $8.600 EUAC minimum truk baru. Berdasarkan data yang ada saat ini, paling ekonomis untuk mempertahankan aset lama selama dua tahun lagi dan selanjutnya menggantinya dengan aset baru.

PERBANDINGAN KETIKA MASA MANFAAT ASET LAMA BERBEDA DENGAN ASET PENGGANTI

Situasi ketiga terjadi ketika masa manfaat aset pengganti terbaik dan aset lama diketahui, atau dapat diestimasi, namun tidak memiliki nilai yang sama.

Ketika asumsi berulangan (repeatability) tidak dapat diterapkan, asumsi berakhir bersamaan (coterminated) dapat digunakan; asumsi ini menggunakan periode studi terbatas untuk semua alternatif. Jika pengaruh inflasi akan dilibatkan dalam analisis penggantian, dianjurkan untuk menggunakan asumsi coterminated.

Contoh

Andaikan kita dihadapkan pada masalah penggantian yang sama dengan contoh di atas, kecuali bahwa periode masa manfaat yang dibutuhkan adalah (a) tiga tahun atau (b) empat tahun. Artinya, periode analisis terbatas dengan menggunakan asumsi coterminated digunakan. Untuk setiap kasus tersebut, alternatif mana yang harus dipilih?

Jawaban :

(a)  Untuk perencanaan tiga tahun, secara intuitif kita akan berpikir apakah aset lama harus dipertahankan tiga tahun lagi ataukah harus segera diganti dengan aset baru untuk digunakan tiga tahun kemudian. EUAC aset lama untuk tiga tahun adalah $7.966 dan EUAC aset baru untuk tiga tahun adalah $8.600. Berdasarkan hal ini, aset lama akan dipertahankan selama tiga tahun. Namun, ini tidaklah tepat. Dengan memfokuskan pada kolom “total biaya (marginal)”, kita dapat melihat bahwa aset lama memiliki biaya paling rendah pada dua tahun pertama, tetapi pada tahun ketiga aset lama ini memiliki biaya sebesar $9.100; sedangkan biaya tahun pertama aset pengganti adalah $9.000. Dengan demikian, akan lebih ekonomis untuk mengganti aset lama setelah tahun kedua. Kesimpulan ini dapat dibuktikan dengan menghitung semua kemungkinan penggantian dan biayanya yang terkait, untuk selanjutnya menghitung EUAC masing-masing.

(b)  Untuk rentang perencanaan empat tahun, alternatif-alternatif tersebut beserta biaya-biayanya yang terkait untuk masing-masing tahun dan EUACnya ada dalam tabel dibawah ini

Penentuan kapan untuk mengganti aset lama dengan rentang rencana empat tahun

Pertahankan aset lama untuk	Pertahankan aset baru untuk	Biaya total (marjinal) untuk setiap tahun				EUAC pada 10% untuk 4 tahun
		1	2	3	4
0 tahun	4 tahun	-$9.000	-$8.250	-$8.495	-$10.850	-$9.082
1	3	-7.000	-9.000	-8.250	-8.495	-8.301
2	2	-7.000	-8.000	-9.000	-8.250	-8.005 ® negatif terkecil
3	1	-7.000	-8.000	-9.100	-9.000	-8.190
4	0	-7.000	-8.000	-9.100	10.000	-8.406

Jadi, alternatif paling ekonomis adalah mempertahankan aset lama selama dua tahun lagi kemudian menggantinya dengan aset baru, untuk dipertahankan dua tahun kemudian. Jika analisis penggantian melibatkan aset lama yang tidak dapat lagi digunakan akibat perubahan teknologi, keharusan perbaikan, dst, maka pilihan diantara dua atau lebih alternatif harus dibuat.

Contoh

Sebuah robot digunakan dalam sebuah laboratorium komersial untuk menangani sampel keramik yang ditempatkan dalam ruang bertemperatur tinggi yang merupakan bagian dari sebuah prosedur pengujian. Karena adanya perubahan kebutuhan konsumen, robot tersebut tidak akan dapat memenuhi persyaratan kebutuhan masa datang. Sedangkan di masa datang akan diperlukan pengujian sampel material keramik yang lebih besar, juga dengan temperatur yang makin tinggi. Kedua perubahan ini akan melebihi kemampuan operasi robot yang ada saat ini.

Karena situasi ini, dua robot berteknologi tinggi telah dipilih untuk dilakukan analisis ekonomi dan perbandingan diantara keduanya. Estimasi berikut ini telah dikembangkan dari informasi yang diberikan oleh beberapa pengguna robot-robot tersebut dan data-data yang diperoleh dari pembuat robot tersebut. MARR sebelum pajak perusahaan adalah 25% per tahun. Berdasarkan informasi ini, robot mana yang secara ekonomi lebih dipilih?

	ROBOT
	R1	R2
Investasi modal harga pembelian	-$38.200	-$51.000
Biaya pemasangan	-2.000	-5.500
Biaya tahunan	-1.400 dalam tahun 1, dan meningkat setelahnya pada tingkat 8%/tahun	-1.000 pada tahun 1, dan meningkat setelahnya pada $150/tahun
Masa manfaat (tahun)	6	110
Nilai pasar	-$1.500	+$7.000

Jawaban :

Asumsi berulangan (repeatability) dengan metode AW digunakan dalam pembandingan kedua robot. Kedua robot tersebut, jika terpilih, diharapkan dapat memberikan jasa yang diinginkan selama periode masa manfaat totalnya. Demikian pula kedua robot paling mungkin akan diganti pada akhir masa hidupnya dengan robot baru pengganti yang lebih baik. Ekuitas biaya tahunan (annual equivalent cost) sebuah penantang baru pada saat itu harus lebih kecil dari model R1 atau R2 dan harus memberikan jasa yang sama atau lebih baik karena perkembangan teknologi yang terus berlanjut serta persaingan diantara pembuat robot.

Estimasi biaya tahunan R1 adalah urutan kas geometris dimulai tahun pertama. Convenience rateyang dibutuhkan untuk menghitung PW urutan ini adalah

icr = (0,25-0,008)/1,08 = 0,1574 atau 15,74%.

Nilai sisa (salvage value) negatif (-$1.500) menunjukkan biaya neto yang diharapkan untuk pelepasan aset pada akhir tahun keenam.

AWR1(25%)     = – ($38.200 + $2.000) (A/P,25%,6) – ($1.400/1,08) (P/A,15,74%,6) – ($1.500) (A/F,25%,6)

= -$15.382

Untuk model R2, AW selama masa manfaatnya adalah

AW (25%)       = – ($51.000 + $5.500) (A/P,25%,10) – [$1.000(P/A,25%,10) + $150(P/G,25%,10)] (A/P,25%,10) +$7.000(A/F,25%,10)

= -$17.035

Robot pengganti R1 secara ekonomis lebih dipilih karena AW selama masa manfaatnya memiliki nilai negatif paling kecil (-$15.382).

Berdasarkan konsep di atas, peran perhitungan ekonomi sangatlah penting dalam segala bidang termasuk dalam pemiihan alat rumah tanngga dan di dunia usaha maupun industri. Penting, di karenakan umur ekonomis bisa berpengaruh dengan penghasilan produksi, laba, investasi dan kemajuan dalam kegiatan ekonomi. Bisa dianalogikan umur ekonomis sebagai pedoman peritungan dalam mengambl keputusan dalan hal kegiatan ekomnomi. Makin kita memperhatikan masalah umur ekonomis, makin kecil kemungkinan kita mengalami kerugian.

BAB 6

6.1 ANALISA REPLACEMENT

Sebuah keputusan seringkali dihadapi oleh perusahaan atau oganisasi pemerintah, maupun oleh setiap individu adalah apakah aset yang ada saat ini harus dihentikan dari penggunaanya dan diganti dengan aset yang baru, atau diteruskan setelah dilakukan perbaikan. Karena tekanan persaingan di era globalisasi yang terus berkembang, maka kebutuhan akan kualitas barang dan jasa yang lebih baik, waktu tanggapan yang lebih cepat, serta perubahan-perubahan yang lain, menyebabkan keputusan seperti di atas makin sering terjadi.

Oleh karena itu, masalah replacement memerlukan analisis yang tepat agar dapat diperoleh informasi yang dibutuhkan untuk membuat keputusan logis yang dapat memperbaiki efisiensi operasi, serta memperkokoh keberadaan perusahaan dalam menghadapi persaingan di era globalisasi sekarang ini.

Dikenal istilah :

-Defender : peralatan / mesin yang ada

-Challenger : pengganti

Prinsip-prinsip dalam Replacement Analysis:

1.Pengeluaran-pengeluaran yang sudah lalu tidak lagi relevan, tidak ditinjau lagi karena sudah lewat.

2.Yang ditinjau adalah : haga pasar (market value) saat ini dan pengeluaran-pengeluaran / penerimaan-penerimaan yag akan dating. Angka-angka yang digunakan mungkin saja berbeda dengan data waktu membeli peralatan yang lama (defender).

SUMBER :

http://abdulhamidbmx.blogspot.com/2012/05/analisi-sensitivitas-analisis-titik.html

repository.upi.edu/operator/upload/s_mat_0706443_chapter3.pdf

http://achmad-amirudin21.blogspot.com/2012/05/analisis-sensitivitas-titik-impas.html

http://repository.upi.edu/operator/upload/s_mat_0706443_chapter3.pdf

http://kuliah-ft.umm.ac.id/pluginfile.php/171/mod_folder/content/1/Ekonomi%20Teknik/bahan-ajar-ekotek.pdf?forcedownload=1

http://abdulhamidbmx.blogspot.com/2012/05/analisi-sensitivitas-analisis-titik.html

http://paybackperiods.blogspot.com/

http://irfanramadhan4.wordpress.com/2011/12/30/umur-ekomonis/

http://saifoemk.lecture.ub.ac.id/files/2012/01/Ekotek9-Replacement-Analysis-Capital-Budgeting.pdf